Blog Post 14

For this blog post we are focusing on variable selection for our linear regression model. First we must divide the dataset using the code below.

Now, we construct a model to work backwards to select our variables. Since my dataset has 116 variables I just picked the 8 that made logical sense to include. The output of my code is provided below.

CODE:

fit = lm (dtrn$int_rate ~ dtrn$annual_inc + dtrn$loan_amnt + dtrn$total_pymnt + dtrn$revol_util + dtrn$dti + dtrn$installment + dtrn$total_acc + dtrn$last_pymnt_amnt)

summary(fit)

I will only take out the least significant variables for my next round. I can also see in my linear regression model that my R- squared value is .3149, this gives us a baseline.

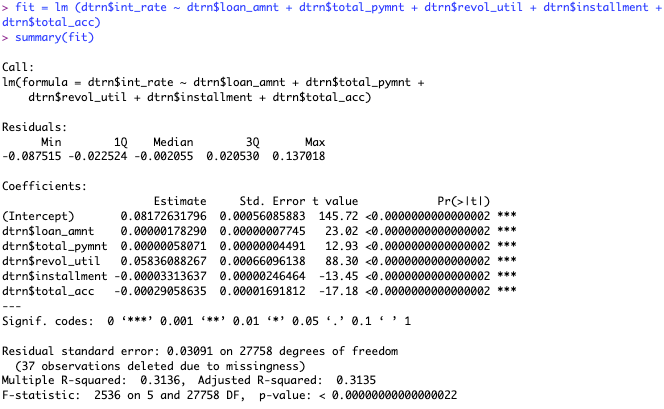
Now all of my variables are significant, but what I didn’t expect was a drop in the R-squared value. The drop is not by much, which most likely helped me because I was overfitting the model. This most likely helped my model be more realistic as I am not using less significant variables. After doing this, I will create my new models with each of the variables in it, creating 16 different models to determine which is the best one. After looking at every single combination, I determined that the one with all of the variables above was the best model based on the R-squared.