In this blog post, I will be using a loan amount and annual income to predict interest rates of a personal loan for the use of credit card payment. I am now using 2 variables in my linear regression model. I ran this code to better predict the interest rate for a loan compared to the last model discussed in post 6.
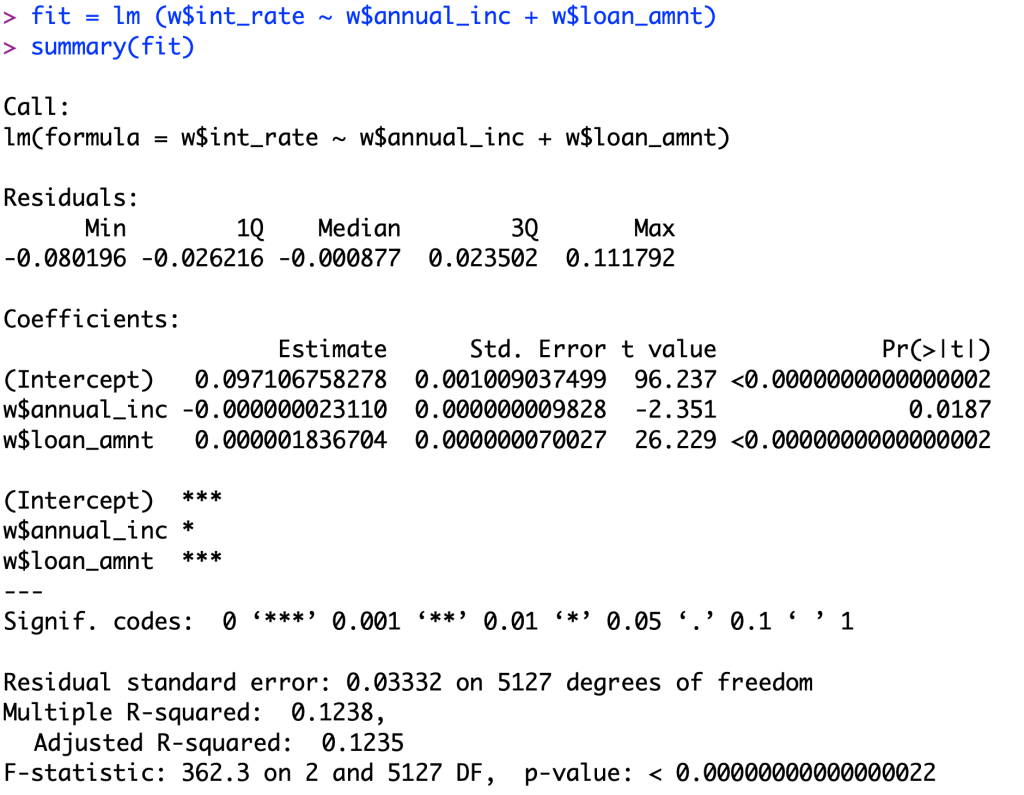
Looking at the p-value, we can see that the even with a alpha value of 0.02, a 95% confidence interval, both our independent variables pass for significance with t values of 26.229 and -2.351. Looking at the second variable, we can see that it is significant, but it is not as good as a relationship compared to our first variable.
In regards to the coefficients, we have a coefficient for annual income of -0.00000002311 which means for every 1 dollar increase in annual income, the interest rate decreases 0.000000023110. To but this in better perspective, for every 10,000 dollars increased it will be a 0.0002311 decrease in the interest rate (0.02311%). Now, looking at the loan amount coefficient we can interpret this number as for every 1 dollar increase in the loan, we will normally see a 0.000001836704 increase in the interest rate. Again to put this into perspective, for every 10000 dollars increase in the loan, you will see an increase in the interest rate of 0.01836704 (1.837%).
When we look at the R-squared value of 0.1238, we can interpret this as 12.38% of the data variation is described by the relationship between the 2 variables tested within our linear regression model. On the other side of this number, we can see that a whopping 87.62% of the data variation is NOT explained by the 2 variables, which leads me to believe that there is some other factor that may be affecting interest rates outside of the dataset. Between this linear regression model and the one shown in post 6, there has been a .07 increase in the R-squared value. This leads me to believe that there is not a huge difference when adding the second variable into the linear regression model, even though the second variable IS significant to interest rates.
Just for fun, we will see what happens if I add a third variable into the set.
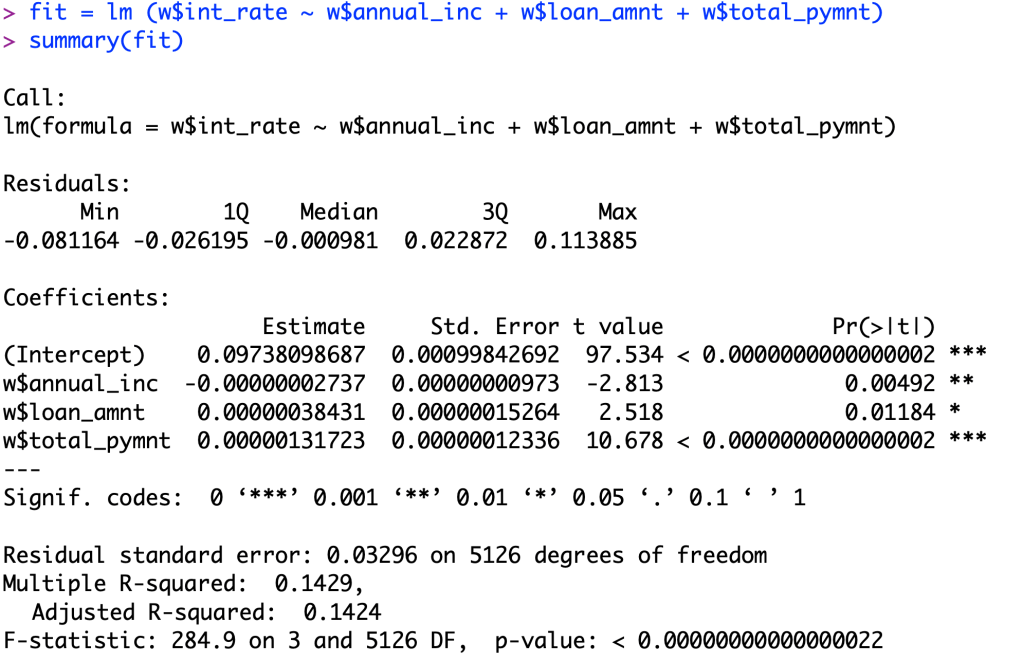
Something that I noticed when I added this third value of total payment is that the R-squared value increased, BUT also decreased the significance of the annual income and loan amount when determining a relationship between the variable and interest rates.